문제
삼각수 Tn(n ≥ 1)는 [그림]에서와 같이 기하학적으로 일정한 모양의 규칙을 갖는 점들의 모음으로 표현될 수 있다.
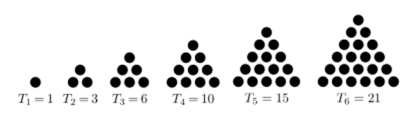
[그림]
자연수 n에 대해 n ≥ 1의 삼각수 Tn는 명백한 공식이 있다.
Tn = 1 + 2 + 3 + ... + n = n(n+1)/2
1796년, 가우스는 모든 자연수가 최대 3개의 삼각수의 합으로 표현될 수 있다고 증명하였다. 예를 들어,
- 4 = T1 + T2
- 5 = T1 + T1 + T2
- 6 = T2 + T2 or 6 = T3
- 10 = T1 + T2 + T3 or 10 = T4
이 결과는 증명을 기념하기 위해 그의 다이어리에 “Eureka! num = Δ + Δ + Δ” 라고 적은것에서 유레카 이론으로 알려졌다. 꿍은 몇몇 자연수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 궁금해졌다. 위의 예시에서, 5와 10은 정확히 3개의 삼각수의 합으로 표현될 수 있지만 4와 6은 그렇지 않다.
자연수가 주어졌을 때, 그 정수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 없는지를 판단해주는 프로그램을 만들어라. 단, 3개의 삼각수가 모두 달라야 할 필요는 없다.
입력
프로그램은 표준입력을 사용한다. 테스트케이스의 개수는 입력의 첫 번째 줄에 주어진다. 각 테스트케이스는 한 줄에 자연수 K (3 ≤ K ≤ 1,000)가 하나씩 포함되어있는 T개의 라인으로 구성되어있다.
출력
프로그램은 표준출력을 사용한다. 각 테스트케이스에대해 정확히 한 라인을 출력한다. 만약 K가 정확히 3개의 삼각수의 합으로 표현될수 있다면 1을, 그렇지 않다면 0을 출력한다.
예제 입력 1 복사
3
10
20
1000
예제 출력 1 복사
1
0
1
출처
ICPC > Regionals > Asia Pacific > Korea > Asia Regional - Daejeon 2014 C번
알고리즘 분류
# https://www.acmicpc.net/problem/10448
import sys
def check(target,alist):
for i in alist:
for j in alist:
for k in alist:
if i+j+k==target:
return 1
return 0
alist=[]
for i in range(1,100):
if i*(i+1)/2>1000:
break
alist.append(i*(i+1)/2)
for i in range(int(sys.stdin.readline())):
print(check(int(sys.stdin.readline()),alist))'알고리즘 문제 > 백준' 카테고리의 다른 글
| 직사각형 네개의 합집합의 면적 구하기 #2669 (0) | 2023.01.04 |
|---|---|
| 슈퍼 마리오 #2851 (0) | 2023.01.04 |
| 오르막길 #2846 (0) | 2023.01.04 |
| 누울 자리를 찾아라 #1652 (0) | 2023.01.04 |
| 약수들의 합 #9506 (0) | 2023.01.04 |