797. All Paths From Source to Target

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

 

Example 1:

Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

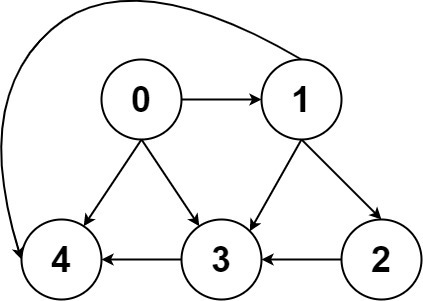
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

 

Constraints:

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i (i.e., there will be no self-loops).
• All the elements of graph[i] are unique.
• The input graph is guaranteed to be a DAG.

---

class Solution:
    def allPathsSourceTarget(self, g: List[List[int]]) -> List[List[int]]:
        ans=[]
        path=[0]
        def dfs(nums):
            if not nums:
                return
            for num in nums:
                path.append(num)
                if num==len(g)-1:
                    ans.append(path.copy())
                dfs(g[num])
                path.pop()
        
        dfs(g[0])
        return ans