Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1:
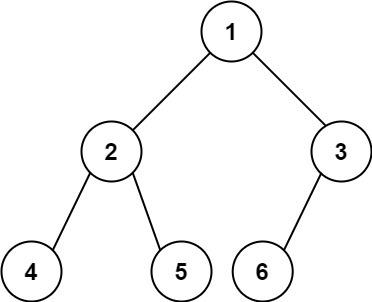
Input: root = [1,2,3,4,5,6]
Output: 6
Example 2:
Input: root = []
Output: 0
Example 3:
Input: root = [1]
Output: 1
Constraints:
- The number of nodes in the tree is in the range [0, 5 * 104].
- 0 <= Node.val <= 5 * 104
- The tree is guaranteed to be complete.
# https://leetcode.com/problems/count-complete-tree-nodes/description/
'''
1. 아이디어 :
1) dfs로 풀 수 있다. 노드가 있으면 ans 배열에 1추가하며 재귀를 호출한다.
2) bfs로 풀 수 있다. ans=0, stack =[]을 선언 후, ans+=1, stack에 left, right를 추가한다.
2. 시간복잡도 :
1) O(n)
- 탐색 시간
2) O(n)
- 탐색 시간
3. 자료구조 :
1) Binary Tree
2) Binary Tree
'''
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
1)
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
ans = []
def dfs(node):
if not node:
return
dfs(node.left)
dfs(node.right)
ans.append(1)
dfs(root)
return sum(ans)
2)
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
ans = 0
stack = [root]
while stack:
node = stack.pop()
ans+=1
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return ans'알고리즘 문제 > Leetcode' 카테고리의 다른 글
| 621. Task Scheduler (0) | 2023.01.31 |
|---|---|
| 965. Univalued Binary Tree (0) | 2023.01.27 |
| 257. Binary Tree Paths (0) | 2023.01.27 |
| 215. Kth Largest Element in an Array (1) | 2023.01.25 |
| 973. K Closest Points to Origin (0) | 2023.01.25 |